Expert Tips: Creep Analysis 4

Creep Analysis 3

The blog article of Creep Analysis 3 showed how Dr. Ghali et al. explained the creep analysis by flexibility methods.

To better understand the creep behavior, solve the previous example in a less efficient way. Here, different sign conventions will be applied.

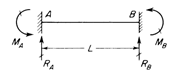
Sign Convention

At time t₀, the immediate displacements/rotations for member 1 due to uniform loads are

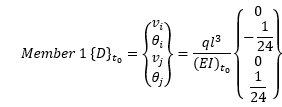
At time t₁, the immediate displacements/rotations due to uniform loads at span 2 are (MIDAS file ex4.2A)

The signs in the table are according to the global axis. Converting into element local axis,

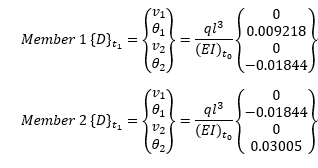
Restrained displacements/rotations are

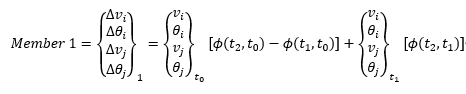
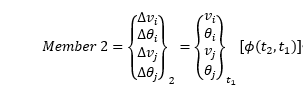
Let

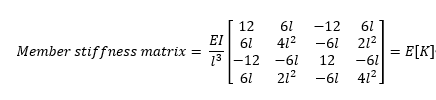
Restrained member end forces are

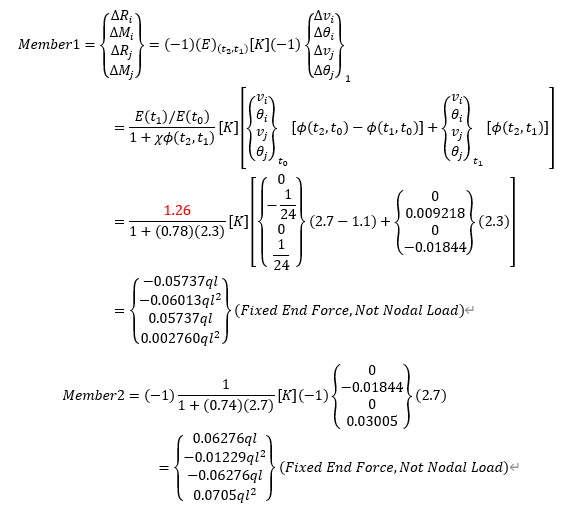
The remaining calculations are the same as the previous example.